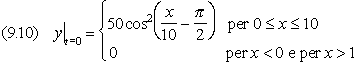|
|
|
| |
|
Esempio 9.1 In una vasca rettangolare lunga 5 m è prodotta un’onda
unidimensionale il cui profilo iniziale (fig.9.9a) è descritto dall’equazione 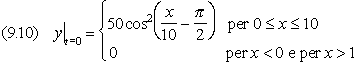
con x e y in cm. Sapendo che l’onda si
propaga nel verso crescente dell’asse x alla velocità v = 1
m/s, senza attenuazione, determinare il suo profilo agli istanti t1= 1 s e t2 = 2 s. Soluzione L’espressione dell’onda a t = 0 può essere
riscritta, mediante le funzioni a gradino, nella forma 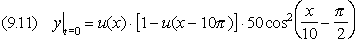
Pertanto, trattandosi di un’onda progressiva con v =
100 cm/s, l’equazione dell’onda, con t in secondi, è 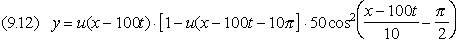
Ponendo in tale espressione t1 = 1 e t2
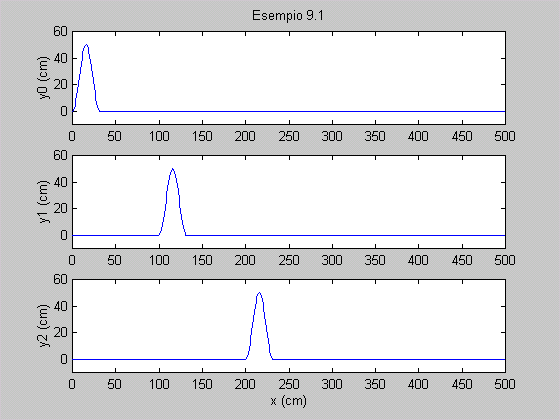
= 2 si ottengono i profili dell’onda nei relativi istanti (fig. 9.9b e c). 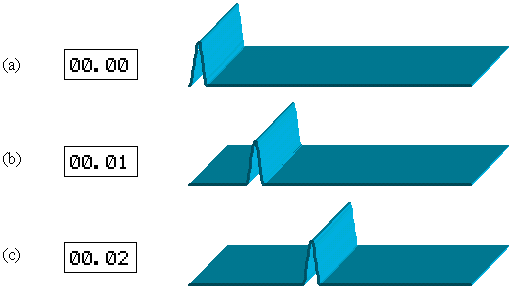
Fig. 9.9 - Esempio 9.1. |
| |
| Definizione del vettore x con valori tra 0 e 500 cm |
x=0:1:500; |
| Definizione del vettore y0 (t = 0) |
y0=stepfun(x,0).*(1-stepfun(x,10*pi))...
.*50.*(cos(x/10-pi/2)).^2; |
| Definizione del vettore y1 (t = 1 s) |
y1=stepfun(x-100,0).*(1-stepfun(x-100,...
10*pi)).*50.*(cos((x-100)/10-pi/2)).^2; |
| Definizione del vettore y2 (t = 2 s) |
y2=stepfun(x-200,0).*(1-stepfun(x-200,...
10*pi)).*50.*(cos((x-200)/10-pi/2)).^2; |
| Suddivisione della figura in tre finestre e selezione della finestra 1 |
subplot(3,1,1) |
| Esecuzione del grafico x - y0 |
plot(x,y0) |
| Cambio di scala sull’asse verticale per assicurare la leggibilità del grafico |
axis([-inf inf -10 60]) |
| Inserimento dell’etichetta sull’asse verticale |
ylabel ('y0 (cm)') |
| Inserimento del titolo |
title('Esempio 9.1') |
| Selezione della finestra 2 |
subplot(3,1,2) |
| Esecuzione del grafico x - y1 |
plot(x,y1) |
| Cambio di scala sull’asse verticale |
axis([-inf inf -10 60]) |
| Inserimento dell’etichetta sull’asse verticale |
ylabel('y1 (cm)') |
| Selezione della finestra 3 |
subplot(3,1,3) |
| Esecuzione del grafico x - y2 |
plot(x,y2) |
| Cambio di scala sull’asse verticale |
axis([-inf inf -10 60]) |
| Inserimento dell’etichetta sull’asse orizzontale |
xlabel('x (cm)') |
| Inserimento dell’etichetta sull’asse verticale |
ylabel('y2 (cm)') | |
| |
| Tab. 1 |
| |
|
|
|
| |
Esempio 9.2 Si consideri un’onda meccanica
bidimensionale uniforme che subisca un’attenuazione del tipo 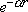 .
Poiché l’intensità, proporzionale al quadrato della perturbazione, decresce
con 1/r per l’allargamento del fronte, l’equazione dell’onda deve
comprendere un ulteriore termine di smorzamento del tipo b/ .
Poiché l’intensità, proporzionale al quadrato della perturbazione, decresce
con 1/r per l’allargamento del fronte, l’equazione dell’onda deve
comprendere un ulteriore termine di smorzamento del tipo b/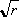 : : 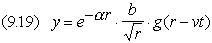
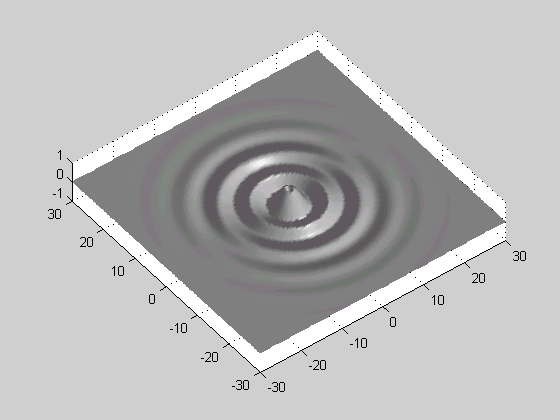
Nel riquadro è
rappresentata un’onda sinusoidale smorzata. |
| |
| Definizione dell’apertura sul piano orizzontale del grafico |
d=30; |
Definizione del coefficiente di smorzamento 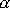 |
alfa=.2; |
| Definizione del vettore a a 120 valori tra -d e d |
a=linspace(-d,d,120); |
| Definizione delle matrici x e y 120
× 120 che individuano il reticolo di punti sul piano orizzontale su cui costruire il grafico |
[x,y]=meshgrid(a); |
| Definizione della matrice r
120 × 120 in cui ogni elemento rappresenta la distanza dall’origine sul piano orizzontale |
r=sqrt(x.^2+y.^2); |
| Definizione della matrice z secondo l’equazione 9.19 per t = 0 (z è la perturbazione verticale) |
z=exp(-alfa*r).*sin(r)./sqrt(r); |
| Esecuzione del grafico 3-D dell’onda |
surfl(x,y,z) |
| Ombreggiatura interpolata del grafico |
shading interp |
| Colorazione della superficie a livelli di grigio |
colormap(gray) |
| Specificazione del punto di vista della superficie (azimuth = -37,5°, elevazione = 80°) |
view(-37.5,80) | |
| |
| Tab. 2 |
| |
|
|
|
| |
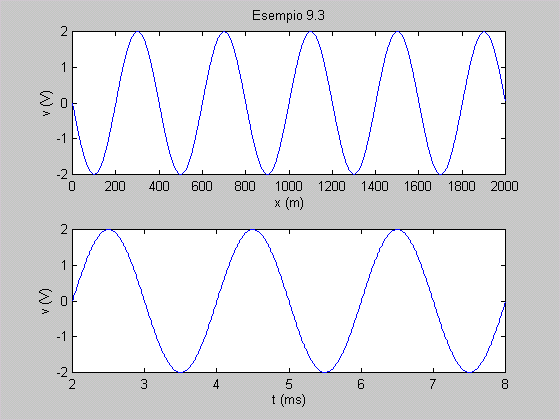
Esempio 9.3 In una linea di trasmissione si
propaga senza attenuazione, a velocità v = 200.000 km/s, una tensione
sinusoidale di ampiezza V = 2 V e lunghezza d’onda 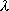 = 400 m. Determinare l’equazione dell’onda, assumendo la fase iniziale
= 400 m. Determinare l’equazione dell’onda, assumendo la fase iniziale  nulla. Rappresentare mediante un grafico l’andamento della tensione per 2 km di linea nell’istante t1
= 1 µs; rappresentare mediante un grafico il valore della tensione in un punto distante d =
1 km dall’origine nell’intervallo di tempo 2 ÷ 8 µs.
nulla. Rappresentare mediante un grafico l’andamento della tensione per 2 km di linea nell’istante t1
= 1 µs; rappresentare mediante un grafico il valore della tensione in un punto distante d =
1 km dall’origine nell’intervallo di tempo 2 ÷ 8 µs. Soluzione Il numero d’onda e la
pulsazione valgono rispettivamente k = 2 / /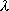 = 15,7 · 10-3 rad/m e
= 15,7 · 10-3 rad/m e  = 2 = 2 f
= 2 f
= 2 v/ v/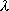 = 3,14 · 106 rad/s; pertanto l’equazione dell’onda è v(x,t)
= 2sen(15,7 · 10-3x · 3,14 · 106t). Il
primo grafico richiesto si ottiene dall’espressione v(x,t1)
= 2sen(15,7 · 10-3x - 3,14 · 106 · 10-6)
= 2sen(15,7 · 10-3x - 3,14) con 0
= 3,14 · 106 rad/s; pertanto l’equazione dell’onda è v(x,t)
= 2sen(15,7 · 10-3x · 3,14 · 106t). Il
primo grafico richiesto si ottiene dall’espressione v(x,t1)
= 2sen(15,7 · 10-3x - 3,14 · 106 · 10-6)
= 2sen(15,7 · 10-3x - 3,14) con 0 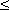 x
x 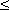 2.000;
il secondo dall’espressione v(d,t) = 2sen(15,7 · 10-3· 103 - 3,14 · 106t) = 2sen(15,7 - 3,14 · 106t)
con 2 · 10-6 2.000;
il secondo dall’espressione v(d,t) = 2sen(15,7 · 10-3· 103 - 3,14 · 106t) = 2sen(15,7 - 3,14 · 106t)
con 2 · 10-6 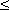 t
t 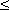 8 ·
10-6. 8 ·
10-6. |
| |
| Definizione del vettore x in m | x=0:1:2000; | | Definizione del vettore v(x,t1) | vx=2*sin(15.7e-3*x-3.14); | | Definizione del vettore t in µs | t=2:.01:8; | | Definizione del vettore v(d,t) | vt=2*sin(15.7-3.14*t); | | Suddivisione della figura in due finestre e selezione della finestra 1 | subplot(2,1,1) | | Esecuzione del grafico x - (x,t1) | plot(x,vx) | | Inserimento dell’etichetta sull’asse orizzontale | xlabel('x (m)') | | Inserimento dell’etichetta sull’asse verticale | ylabel('v (V)') | | Inserimento del titolo | title('Esempio 9.3') | | Selezione della finestra 2 | subplot(2,1,2) | | Esecuzione del grafico t - v(d,t) | plot(t,vt) | | Inserimento dell’etichetta sull’asse orizzontale | xlabel('t (ms)') | | Inserimento dell’etichetta sull’asse verticale | ylabel('v (V)') | |
| |
| Tab. 3 |
| |
|
|
|
| |
Esempio 9.4 Si consideri una corda fissata
alle estremità, di lunghezza l = 1 m. Sapendo che la velocità di
propagazione delle onde nella corda è v = 103 m/s,
determinare la lunghezza d’onda e la frequenza del 4° modo di oscillazione
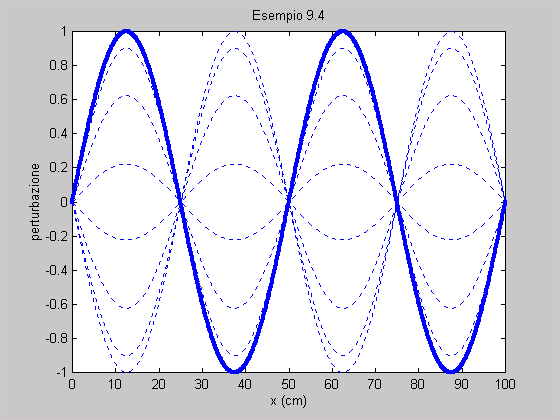
della corda. Rappresentare graficamente la conformazione della corda in istanti
successivi di tempo. Soluzione La lunghezza d’onda del 4°
modo di oscillazione è 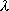 4 =
2l/4 = 0,5 m, a cui corrisponde la frequenza f4 = v/ 4 =
2l/4 = 0,5 m, a cui corrisponde la frequenza f4 = v/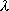 4
= 2 kHz. I movimenti della corda sono rappresentati nel riquadro. 4
= 2 kHz. I movimenti della corda sono rappresentati nel riquadro. |
| |
| Definizione del vettore x in cm |
x=0:.1:100; |
Definizione del vettore y = sen[(2 / /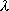 )x] che rappresenta la perturbazione all’istante t = 0 )x] che rappresenta la perturbazione all’istante t = 0 |
y=sin((2*pi/50)*x); |
| Esecuzione del grafico x - y in linea spessa |
plot(x,y,'.') |
| Mantenimento dei grafici in modo che i successivi tracciati non si sostituiscano l’uno con l’altro |
hold |
| Inserimento dell’etichetta sull’asse orizzontale |
xlabel('x (cm)') |
| Inserimento dell’etichetta sull’asse verticale |
ylabel('perturbazione') |
| Inserimento del titolo | title('Esempio 9.4') |
| Definizione del vettore t a 8 valori tra 0 e 0,25 (0,25 ms è la metà del periodo dell’onda) |
t=linspace(0,.25,8); |
Per a = 2, 3, ..., 8 generazione e grafico tratteggiato del vettore y = sen[(2 / /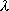 )x]cos[2 )x]cos[2 f · t(a)] che rappresenta l’onda stazionaria nella corda f · t(a)] che rappresenta l’onda stazionaria nella corda t(a) rappresenta l’a-esimo elemento del vettore t |
for a=2:8
y=sin((2*pi/50)*x)*cos(2*pi*2*t(a));
plot(x,y,':')
end | |
| |
| Tab. 4 |
| |
|
|
|