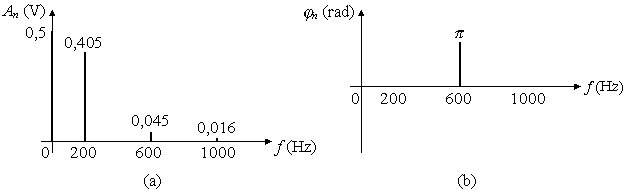|
|
|
| |
|
Esercizio 3.7 Determinare lo sviluppo
in serie di Fourier di un segnale ad onda quadra avente le seguenti
caratteristiche: livello inferiore Vmin = -0,5 V; livello
superiore Vmax = 1,5 V; periodo T = 15 ms. Eseguire
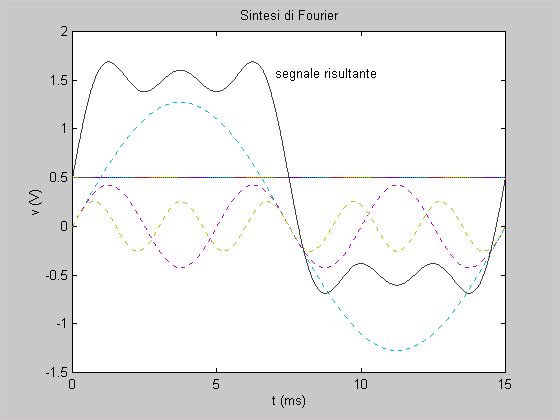
una tabella relativa ai valori dei seguenti segnali presi in un periodo:
componente continua, prime tre armoniche non nulle (n = 1, n = 3, n= 5), segnale risultante dalla somma dei segnali precedenti. Eseguire un grafico
in cui siano raffigurati, con colori diversi, i diversi segnali. Se l’esercizio
è stato svolto correttamente, si dovrà avere il risultato riportato nel
riquadro MATLAB. Lo sviluppo in serie i
Fourier dell’onda quadra è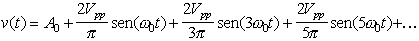 
In questo caso si ha  0
= [2 /15] · 103, A0 = (Vmax
+ Vmin)/2 = 0,5 V e Vpp= 2 V. |
| |
| Definizione della pulsazione del segnale, in krad/s | om0=(2*pi)/15; | | Definizione dell’ampiezza A1 della prima armonica | a1=4/pi; | | Definizione del vettore t in ms | t=0:.01:15; | | Definizione del valor medio A0 del segnale | a0=.5; | | Definizione del vettore prima armonica | v1=a1*sin(om0*t); | | Definizione del vettore terza armonica | v3=(a1/3)*sin(3*om0*t); | | Definizione del vettore quinta armonica | v5=(a1/5)*sin(5*om0*t); | | Definizione del vettore segnale risultante | v=a0+v1+v3+v5; | | Esecuzione nella stessa figura dei grafici dei segnali precedentemente definiti, con le armoniche a linea tratteggiata | plot(t,a0,t,v1,':',t,v3,':',...
t,v5,':',t,v) | | Inserimento dell’etichetta sull’asse orizzontale | xlabel('t (ms)') | | Inserimento dell’etichetta sull’asse verticale | ylabel('v (V)') | | Inserimento del titolo | title('Sintesi di Fourier') | | Posizionamento di testo mediante mouse | gtext('segnale risultante') | |
| |
| Tab. 1 |
| |
|
|
|
| |
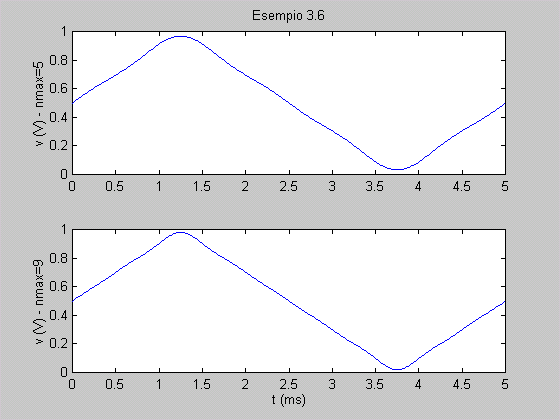
Esempio 3.6 Lo sviluppo in serie di
Fourier del segnale triangolare rappresentato in fig. 3.25 ha la forma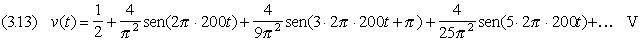 
dove f0
= 1/T = 200 Hz è la frequenza di v(t). Determinare la
rappresentazione del segnale nel dominio della frequenza limitatamente alle
prime tre armoniche non nulle; verificare la corrispondenza tra v(t)
e la serie di Fourier troncata rispettivamente a n = 5 e n = 9.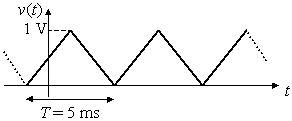 
Fig. 3.25 - Esempio 3.6. Soluzione Lo spettro delle
ampiezze limitato alle prime tre armoniche non nulle comprende la componente
continua, la armonica fondamentale, a 200 Hz, e le successive armoniche di
ordine dispari, a 600 e 1000 Hz (fig. 3.26a); nello spettro delle fasi compare
una sola riga, dato che solo la terza armonica, a 600 Hz, ha fase iniziale
diversa da zero (fig. 3.26b).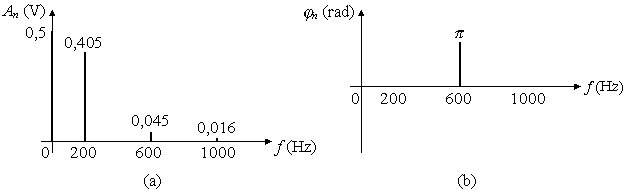 
Fig. 3.26 - Spettri del
segnale di fig. 3.25. |
| |
| Definizione della pulsazione del segnale, in krad/s (T vale 5 ms) | om0=(2*pi)/5; | | Definizione dell’ampiezza A1 della prima armonica | a=4/(pi^2); | | Definizione del vettore t in ms | t=0:.01:5; | | Suddivisione della figura in due finestre e selezione della finestra 1 | subplot(2,1,1) | | Definizione del vettore v5 risultante dalla somma della componente continua e delle armoniche sino a n = 5 | v5=.5+a*sin(om0*t)+(a/9)*sin(3*om0*t...
+pi)+(a/25)*sin(5*om0*t); | | Esecuzione del grafico t - v5 | plot(t,v5) | | Inserimento dell’etichetta sull’asse verticale | ylabel('v (V) - nmax=5') | | Inserimento del titolo | title('Esempio 3.6') | | Selezione della finestra 2 | subplot(2,1,2) | | Definizione del vettore v9 risultante dalla somma della componente continua e delle armoniche sino a n = 9 | v9=v5+(a/49)*sin(7*om0*t+pi)+...
(a/81)*sin(9*om0*t); | | Esecuzione del grafico t - v9 | plot(t,v9) | | Inserimento dell’etichetta sull’asse orizzontale | xlabel('t (ms)') | | Inserimento dell’etichetta sull’asse verticale | ylabel('v (V) - nmax=9') | |
| |
| Tab. 2 |
| |
|
|
|
| |
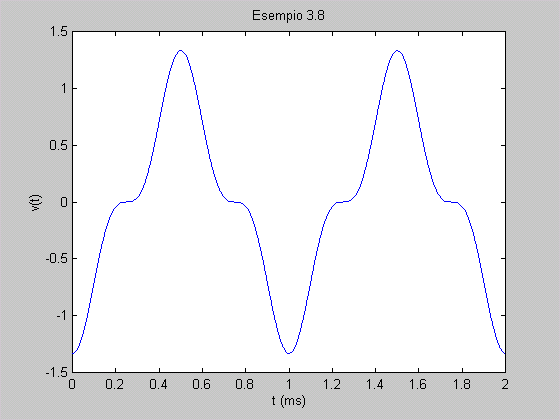
Esempio 3.8 Un’onda quadra a frequenza f0 = 1 kHz e
valor medio nullo attraversa un canale la cui banda passante si estende da 200 a
4.000 Hz. Determinare la forma d’onda del segnale di uscita, ipotizzando che
lo sfasamento introdotto dal canale di trasmissione sia pari a -/2
a tutte le frequenze. Soluzione Il segnale di ingresso ha componenti armoniche a 1, 3, 5,
... kHz. Le frequenze di taglio hanno un valore sufficientemente lontano dalla
frequenza delle prime due componenti, per cui si può supporre che queste
ultime ricadano nella zona a massimo guadagno; per lo stesso motivo assumeremo
che per le componenti da 5 kHz in su il guadagno sia nullo. Il segnale di uscita
ha quindi una forma d’onda risultante dalle prime due componenti del segnale
di ingresso sfasate di /2, con un fattore di
scala che dipende dall’ampiezza picco-picco dell’onda quadra e dal guadagno
a centro banda del canale; non conoscendo queste ultime grandezze, per tracciare
con un grafico la forma d’onda assegniamo un valore a piacere a A1, da cui
consegue A3 = A1/3. |
| |
| Definizione del vettore t in ms (2 cicli) | t=0:.001:2; | | Definizione del vettore vo | Vo=sin(2*pi*t-(pi/2))+...
(1/3)*sin(6*pi*t-(pi/2)); | | Esecuzione del grafico t - vo | plot(t,Vo) | | Inserimento dell’etichetta sull’asse orizzontale | xlabel('t (ms)') | | Inserimento dell’etichetta sull’asse verticale | ylabel('v(t)') | | Inserimento del titolo | title('Esempio 3.8') | |
| |
| Tab. 3 |
| |
|
|
|