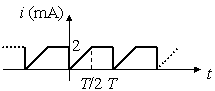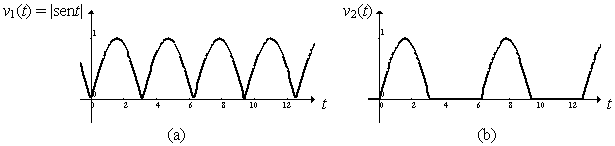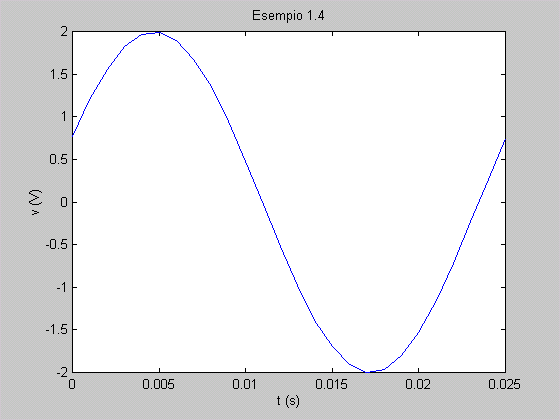
|
|
|
|
Esempio 1.4 Eseguire per punti, nell’intervallo di tempo di un
periodo, il grafico della tensione sinusoidale v(t) = 2sen(251t
+  /8). Soluzione La pulsazione del segnale è  =
251 rad/s, e pertanto il suo periodo vale T = 2/
= 0,025 s =
25 ms. E’ possibile quindi costruire una tabella di punti ad intervalli di 1 ms,
inserendo nell’espressione della funzione valori di t pari a 0 - 0,001 - 0,002
- ..., ottenendo v(0) = 0,765, v(1) = 1,20, v(2) = 1,56, etc.
Unendo i punti si ottiene il grafico rappresentato nel riquadro sottostante. |
| |
| Definizione del vettore t a 26 valori partendo da 0 sino a 25 ms con passo di 1 ms (0 - 0,001 - 0,002 - ... - 0,025 s) | t=0:.001:.025; | | Definizione del vettore v = 2sen(251t + /8) | v=2*sin(251*t+pi/8); | | Esecuzione del grafico t - v | plot(t,v) | | Inserimento dell’etichetta sull’asse orizzontale | xlabel('t (s)') | | Inserimento dell’etichetta sull’asse verticale | ylabel('v (V)') | | Inserimento del titolo | title('Esempio 1.4') | |
| |
| Tab. 1 |
| |
|
|
|
| |
|
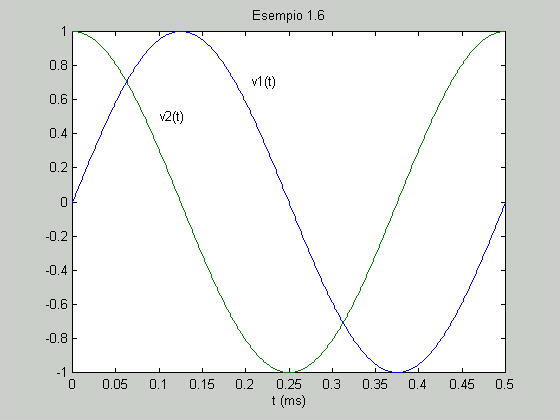
Esempio 1.6 Eseguire su uno stesso piano il grafico di due segnali
sinusoidali in quadratura di fase a frequenza f = 2 kHz. Determinare lo spostamento
temporale tra i due segnali. Soluzione Due segnali sono in quadratura di fase quando lo sfasamento reciproco
è pari a /2. Una possibile scelta dei valori di fase iniziale è
 1 = 0, 2 =
/2. Lo spostamento temporale è pari a t12 = (0 -
/2)/(2
· 2 · 103) = - 0,125
ms (v1 in ritardo su v2). |
| |
| Il periodo dei segnali è T = 1/f = 0,5 ms. Pertanto si può definire il vettore t, direttamente in ms, assegnando valori da 0 a 0,5 con passo 0,001 |
t=0:.001:.5; |
| Definizione del vettore v1 = sen(2 · 2000 · t). Poiché i valori di t sono espressi in millisecondi, e sono quindi 103 volte più grandi di quanto dovrebbero, si deve dividere la pulsazione per 103 e pertanto si ottiene v1 = sen[4 · t(ms)] |
v1=sin(4*pi*t); |
| Definizione del vettore v2 = sen(2 · 2000 · t + /2) |
v2=sin(4*pi*t+pi/2); |
| Esecuzione sullo stesso piano dei grafici t - v1 e t - v2 |
plot(t,v1,t,v2) |
| Inserimento dell’etichetta sull’asse orizzontale |
xlabel('t (ms)') |
| Inserimento del titolo | title('Esempio 1.6') |
| Posizionamento di testo mediante mouse |
gtext('v1(t)') |
| Posizionamento di testo mediante mouse |
gtext('v2(t)') | |
| |
| Tab. 2 |
| |
|
|
|
| |
| Esempio 1.8 Determinare un’espressione analitica per il primo ciclo della
corrente periodica a 100 Hz rappresentata in fig. 1.25.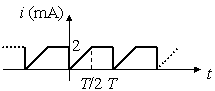 
Fig. 1.25 - Esempio 1.8. Soluzione Il periodo del segnale è pari a T = 1/f = 10 ms.
Scegliamo di rappresentare il ciclo indicato, che va da 0 a T, esprimendo il
tempo in millisecondi (ms) e la corrente in milliampère (mA). Dall’origine al punto
(5; 2) il segnale ha un
andamento lineare rappresentato dall’espressione il = (2/5)t.
Mentre l’andamento per t < 0 non interessa il nostro studio, osserviamo
che in T/2 = 5 ms la forma d’onda cambia, ed è pertanto necessario
moltiplicare il per un gradino di ampiezza unitaria che commuta verso
il basso in T/2 = 5 ms, ottenendo i1 = (2/5)t · [1 - u(t - 5)]. Sommando ora a i1un gradino di ampiezza 2 che commuta verso l’alto in T/2 = 5 ms si ottiene
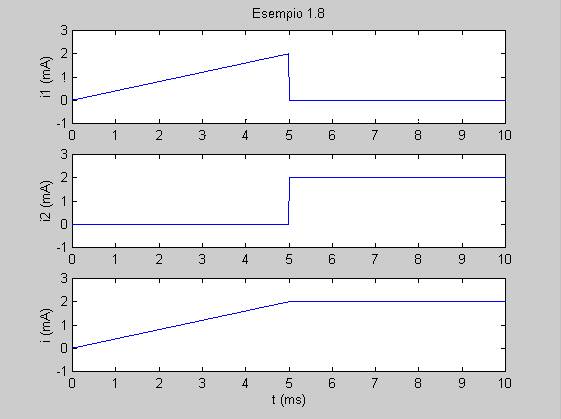
l’espressione finale: i(t) = (2/5)t ·
[1 - u(t - 5)] + 2u(t - 5); i relativi grafici sono
rappresentati nel riquadro sottostante. |
| |
| Definizione del vettore t | t=0:.01:10; | | Definizione del vettore i1 = (2/5)t · [1 - u(t - 5)] | i1=(2/5)*t.*(1-stepfun(t,5)); | | Definizione del vettore i2 = 2u(t - 5) | i2=2*stepfun(t,5); | | Definizione del vettore i | i=i1+i2; | | Suddivisione della figura in tre finestre e selezione della finestra 1 | subplot(3,1,1) | | Esecuzione del grafico t - i1 | plot(t,i1) | | Cambio di scala sull’asse verticale per assicurare la leggibilità del grafico | axis([-inf inf -1 3]) | | Inserimento dell’etichetta sull’asse verticale | ylabel('i1 (mA)') | | Inserimento del titolo | title('Esempio 1.8') | | Selezione della finestra 2 | subplot(3,1,2) | | Esecuzione del grafico t - i2 | plot(t,i2) | | Cambio di scala sull’asse verticale | axis([-inf inf -1 3]) | | Inserimento dell’etichetta sull’asse verticale | ylabel('i2 (mA)') | | Selezione della finestra 3 | subplot(3,1,3) | | Esecuzione del grafico t - i | plot(t,i) | | Cambio di scala sull’asse verticale | axis([-inf inf -1 3]) | | Inserimento dell’etichetta sull’asse orizzontale | xlabel('t (ms)') | | Inserimento dell’etichetta sull’asse verticale | ylabel('i (mA)') | |
| |
| Tab. 3 |
| |
La funzione stepfun(t,t0)restituisce
un vettore della stessa lunghezza di ti cui elementi sono pari a zero se il corrispondente elemento di tè minore di t0,
a uno altrimenti: t=[1 2 3 4 5 6 7 8 9 10];
stepfun(t, 8) <Invio>
ans =
0 0 0 0 0 0 0 1 1 1 |
| |
|
|
|
| |
Esempio sul valore medio di una funzione Determinare il valore medio della funzione v(t)
= sen(4t) · cost · (1 - 0,4t) + 1 nell'intervallo 0 ÷ 16
dapprima su 8 punti, poi su 16.000 punti. |
| |
| Definizione del vettore t a 8 valori centrati negli 8 intervalli 0 ÷ 2, 2 ÷ 4, etc. |
t=1:2:15; |
| Definizione del vettore v(t) |
v=sin(.4*t).*cos(t).*(1-.04*t)+1; |
| Calcolo del valore medio degli elementi del vettore v |
mean(v) |
| output | ans =
0.9667 |
| Definizione del vettore t a 16.000 valori |
t=linspace(0,16,16000); |
| Definizione del vettore v(t) |
v=sin(.4*t).*cos(t).*(1-.04*t)+1; |
| Calcolo del valore medio degli elementi del vettore v |
mean(v) |
| output | ans =
0.9588 | |
| |
| Tab. 4 |
|
| |
Esempio 1.10 Determinare per punti il valore medio dei segnali
rappresentati in fig. 1.29a e b.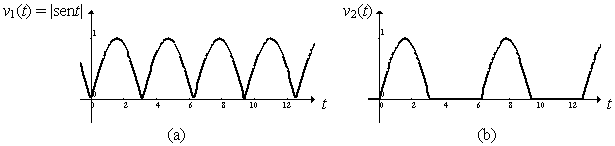 
Fig. 1.29 - Sinusoide raddrizzata (a) a doppia
semionda e (b) a una semionda. Soluzione Nel primo caso è sufficiente determinare la media della
funzione sent nel primo semiperiodo, ottenendo (vedi riquadro
sottostante) <v1> = 0,6366 V. Nel secondo caso la media
del secondo semiperiodo del segnale è nulla, pertanto si ha <v2>
= (<v1> + 0)/2 = 0,3183 V. Il valore medio esatto dei
segnali considerati, calcolato con metodi analitici, è pari rispettivamente a 2V/
e V/, essendo V il valore
massimo del segnale. |
| |
| Definizione del vettore t a 16.000 valori tra 0 e | t=linspace(0,pi,16000); | | Calcolo del valore medio degli elementi del vettore sent | mean(sin(t)) | | Output | ans =
0.6366 | |
| |
| Tab. 5 |
|
| |
Esempio 1.11 Calcolare il v.q.m. e il v.e. della corrente rappresentata in
fig. 1.25. Soluzione L’intervallo di riferimento scelto è 0 - T. Nel
primo semiperiodo il segnale ha un andamento lineare rappresentato dall’espressione
il = (2/5)t, quindi per ottenere il v.q.m. è
necessario eseguire una media per punti della funzione il2
= (4/25)t2 nell’intervallo 0 - 5 ms; il risultato (vedi
riquadro sottostante) è pari a 1,3334 mA2. Nel secondo semiperiodo l’andamento
è costante, per cui il v.q.m. è pari a 4 mA2. Il v.q.m. del segnale è pari alla media dei valori calcolati
nei due semiperiodi: Iq = (1,3334 + 4)/2 = 2,6667 mA2.
Il v.e. è quindi pari a  . |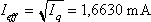
| |
| Definizione del vettore t a 16.000 valori tra 0 e 5 | t=linspace(0,5,16000); | | Definizione del vettore il | i=(2/5)*t; | | Calcolo del valor medio dei quadrati degli elementi del vettore il (v.q.m.) | vq=mean(i.^2) | | Output | vq =
1.3334 | |
| |
| Tab. 6 |
|