Il nome MATLAB deriva da MATrix LABoratory, il che indica come originariamente il programma sia stato sviluppato per essere utilizzato nell’ambito della teoria delle matrici e dell’algebra lineare. Sebbene le caratteristiche di MATLAB siano ormai molto più estese rispetto alle finalità iniziali, l’elemento base per molte delle sue funzioni rimane la matrice. Cos’è una matrice? Si definisce matrice una tabella di p · q numeri disposti su p righe e  q colonne:

Questo è un esempio di matrice 2 × 3: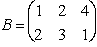

Questo è invece un esempio di matrice 2 × 2: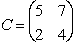

Quando una matrice ha lo stesso numero di righe e di colonne, come nel caso precedente, la matrice è detta quadrata. Data una matrice A, è definita matrice trasposta di A la matrice A’ che si ottiene trasformando le righe di A in colonne. Ad esempio la trasposta della matrice B precedentemente definita è

Se due matrici hanno rispettivamente lo stesso numero di righe e di colonne, sono definite le matrici somma e differenza, ottenute sommando o sottraendo tra loro gli elementi corrispondenti delle due matrici. Ad esempio si ha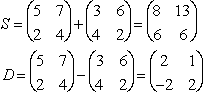

Vogliamo ora affrontare alcuni aspetti della moltiplicazione e divisione tra matrici, pur senza entrare nei dettagli di tali operazioni; ciò è necessario perché, anche non utilizzando matrici vere e proprie, se il codice non è corretto all’esecuzione del codice stesso possono essere generati messaggi di errore riguardanti le dimensioni delle matrici.

Tra due matrici A e B, è definita l’operazione di prodotto A · B solo se il numero di colonne di A è uguale al numero di righe di B (per esempio A è 3 × 2 e B è 2 × 4). Si deve rimarcare che la matrice A · B non si ottiene moltiplicando tra loro gli elementi corrispondenti delle due matrici. Si tenga presente il messaggio di errore che MATLAB restituisce se si tenta di moltiplicare tra loro due matrici le cui dimensioni non lo consentono:

Inner matrix dimensions must agree. (Le dimensioni interne delle matrici devono accordarsi)

Da quanto detto sul prodotto tra matrici deriva che una matrice può essere moltiplicata per sé stessa una o più volte solo se essa è quadrata. Si tenga presente il messaggio di errore che MATLAB restituisce se si tenta di elevare a potenza una matrice non quadrata:

Matrix must be square. (La matrice deve essere quadrata)

Tra due matrici A e B è definita l’operazione di divisione A/B solo se A e B hanno lo stesso numero di colonne. Si deve rimarcare che la matrice A/B non si ottiene dividendo tra loro gli elementi corrispondenti delle due matrici. Si tenga presente il messaggio di errore che MATLAB restituisce se si tenta di eseguire la divisione tra matrici le cui dimensioni non lo consentono:

Matrix dimensions must agree. (Le dimensioni delle matrici devono accordarsi)

Vettori

Una matrice che ha una sola riga è definita vettore. Questo è un esempio di vettore a 8 valori:

V = (1 3 5 6 -2 4 -3 9)

Più che con le matrici, nell’utilizzo di MATLAB avremo a che fare con i vettori. Ad esempio volendo costruire il grafico di una funzione y = f(x) nell’intervallo x₁ ÷ x₂ è necessario definire un insieme di valori della variabile x in tale intervallo e un corrispondente insieme di valori della variabile y. Analogamente, per calcolare la media della stessa funzione nell’intervallo considerato è necessario applicare l’operazione di media al vettore che rappresenta i valori di y. Quello che è importante rimarcare è che MATLAB interpreta i vettori come matrici 1 × q; se per esempio il codice contiene l’elevazione a potenza di un vettore, MATLAB restituirà il messaggio di errore

Matrix must be square.

Scalari

Si definisce scalare una variabile rappresentata esclusivamente con un numero. Questo è un esempio di scalare:

a = 5

Si noti che MATLAB non interpreta uno scalare come una matrice 1 × 1; se per esempio si moltiplica uno scalare a per una matrice o un vettore, MATLAB non restituisce un messaggio di errore, ma provvede a moltiplicare tutti gli elementi della matrice o del vettore per a.